Might a Single Neuron Solve Interesting Machine Learning Problems Through Successive Computations on Its Dendritic Tree?

Abstract

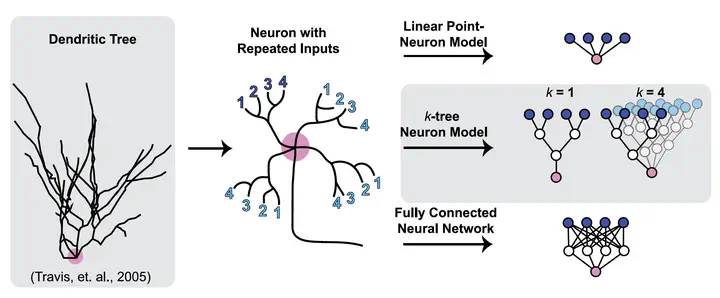
Physiological experiments have highlighted how the dendrites of biological neurons can nonlinearly process distributed synaptic inputs. However, it is unclear how aspects of a dendritic tree, such as its branched morphology or its repetition of presynaptic inputs, determine neural computation beyond this apparent nonlinearity. Here we use a simple model where the dendrite is implemented as a sequence of thresholded linear units. We manipulate the architecture of this model to investigate the impacts of binary branching constraints and repetition of synaptic inputs on neural computation. We find that models with such manipulations can perform well on machine learning tasks, such as Fashion MNIST or Extended MNIST. We find that model performance on these tasks is limited by binary tree branching and dendritic asymmetry and is improved by the repetition of synaptic inputs to different dendritic branches. These computational experiments further neuroscience theory on how different dendritic properties might determine neural computation of clearly defined tasks.

Ilenna Jones

Research Fellow

My research interests include neuronal biophysics, dendritic computation, and neuroscience for AI.